La nuance entre l'intégration au sens de Riemann et au sens de Lebesgue

La nuance entre l'intégration au sens de Riemann et au sens de Lebesgue








Le schéma général utilisé pour construire une intégrale et qui
cherche à mesurer l'aire du domaine sous la courbe, est le même pour les
trois approches de l'intégration, au sens de Riemann, au sens de
Lebesgue, ou au sens de Kurzweil-Henstock.

D'abord, on considère une famille de fonctions élémentaires, pour
lesquelles nous avons un moyen évident de mesurer l'aire sous la courbe.
Dans le cas de l'intégrale de Riemann ou de Kurzweil-Henstock, ce sont
les fonctions en escalier
dont l'aire sous la courbe est égale à la somme des aires des
rectangles ; les fonctions en escalier étant constantes sur des
intervalles, le domaine sous la courbe d'une telle fonction peut alors
être vu comme une réunion de rectangles. Pour l'intégrale de Lebesgue,
les fonctions élémentaires sont les fonctions étagées, constantes, non plus sur
des intervalles, mais sur des parties mesurables (approche plus souple et
plus générale).

Intégrale de
Kurzweil-Henstock

• Soit [a, b] un segment de .
  On appelle subdivision marquée de [a, b] tout
  couple de familles finies de points
  et
  telles que
  
  On
  dit que
  marque le segment .
  

• Si
  est une fonction définie sur [a, b] à valeurs strictement
  positives, on dit que
  est une jauge (sur [a, b]), et la subdivision est
  dite plus fine que
  si
  

Un théorème important, le lemme de Cousin, est fréquemment utilisé dans la théorie de
la KH-intégration ; il affirme que, quelle que soit la jauge choisie, il
existe des subdivisions marquées plus fine que cette jauge.

• Une fonction f bornée ou non sur un segment [a, b],
  à valeurs réelles ou complexes, est intégrable au sens de
  Kurzweil-Henstock (ou KH-intégrable), d'intégrale A, si
  
  il existe une jauge
  telle que, pour toute subdivision
  marquée par
  plus fine que ,
  on a :
  
  A
  est alors unique et s'appelle l'intégrale de f sur [a, b].
  On la note alors
  

• La quantité
  s'appelle somme de Riemann de f relativement à la
  subdivision marquée choisie.
  

On remarque que, si on prend des jauges
constantes, on retrouve la définition de l'intégrale de Riemann. La KH-intégrale
consiste à remplacer ces jauges constantes par des jauges variables.

• Dans le cas où f est définie sur un intervalle I
  qui n'est pas un segment, on dit que f est KH-intégrable
  d'intégrale A, si
  ,
  il existe une jauge
  et un nombre ,
  tels que, pour toute subdivision
  marquée par ,
  plus fine que
  sur tout segment contenant
  on a :
  
  

Propriétés [modifier]

• L'ensemble des fonctions KH-intégrables forme un espace
  vectoriel et l'intégrale est une forme linéaire positive sur cet espace.
  
• Toute fonction Riemann-intégrable ou Lebesgue-intégrable est KH-intégrable
  avec la même intégrale ; en particulier, la fonction de Dirichlet valant 1 sur les
  rationnels et 0 sur les irrationnels, n'est pas Riemann-intégrable,
  mais est KH-intégrable d'intégrale nulle.
  
• De même, la fonction
  sur
  n'est pas Lebesgue-intégrable, mais c'est une intégrale (au sens de
  Riemann) impropre convergente, et elle est donc KH-intégrable
  (d'intégrale ;
  il s'agit de l'intégrale de Dirichlet).
  Contrairement aux fonctions Lebesgue-intégrables, une fonction peut être
  KH-intégrable sans que sa valeur absolue le soit.
  
• Une fonction
  est Lebesgue-intégrable si et seulement si
  et
  sont KH-intégrables (ce qui permet de définir la notion d'ensemble
  mesurable (pour la mesure de Lebesgue) comme un ensemble dont la fonction
  caractéristique est KH-intégrable). Il ne suffit pas que
  soit KH-intégrable pour que
  le soit. Si
  est KH-intégrable et si
  est majorée par une fonction KH-intégrable, alors
  est KH-intégrable.
  
• Le théorème fondamental de
  l'analyse s'exprime comme suit :
  
  
  
  • Soit
    dérivable sur
    de dérivée .
    Alors
    est KH-intégrable et
    
  • Soit
    KH-intégrable. Alors la fonction
    est continue et admet presque partout
    une dérivée égale à .
    
  
  


• La notion d'intégrale impropre est inutile avec la
  KH-intégrale. En effet, soit
  est une fonction définie sur
  et telle que, pour tout
  élément de ,
  
  est KH-intégrable sur .
  Si
  existe et vaut ,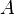
  alors
  est KH-intégrable sur
  et son intégrale vaut .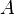
  
• Le théorème de convergence
  monotone et le théorème de convergence dominée
  sont vrais avec la KH-intégrale, ce dernier devenant plus précisément
  un théorème de convergence encadrée (la raison étant que
  l'intégrabilité de
  n'entraîne pas celle de ).
  

L'intégrale de Riemann permet d'intégrer entre autres les fonctions
croissantes ou décroissantes, et les fonctions continues, donc aussi les
fonctions continues par morceaux, ainsi que les fonctions monotones par
morceaux. Toute limite uniforme de fonction intégrables au sens de
Riemann est intégrable au sens de Riemann. Cependant une limite simple
(c'est-à-dire f(x) = lim f_n(x)
pour tout x de l'intervalle [a,b] sans condition d'uniformité
en x) de fonctions Riemann
intégrables n'est pas nécessairement Riemann intégrable. Il est possible
de caractériser les fonctions intégrables au sens de Riemann : ce sont
les fonctions bornées dont l'ensemble des points de discontinuité est de
mesure nulle (critère de Lebesgue). L'intégration au
sens de Lebesgue permet d'intégrer plus de fonctions (dont des
fonctions qui ne sont même pas localement bornées), et elle donne la
même valeur à l'intégrale lorsque la fonction est déjà intégrable au
sens de Riemann. Elle a l'avantage de munir l'espace vectoriel des
fonctions intégrables (modulo l'égalité presque partout) d'une structure
d'espace normé complet. Ceci est essentiel pour beaucoup
d'applications. Cependant, on perd la notion de sommes de Riemann, et il
existe des contextes (étude des suites uniformément distribuées par
exemple) où les fonctions intégrables au sens de Riemann surviennent
naturellement ; pour une généralisation de cette dernière permettant
néanmoins d'intégrer également toutes les fonctions mesurables (au sens
de Lebesgue)